F100計算-2の課題「上昇限度が2,000~3,000m大きい」の解決を試みます
※本ブログは、「F100-PW-100ターボファンの計算-3」を改題したのです。
「F100ターボファンの計算-1「海面上静止推力」」で、海面上、標準大気、静止状態のエンジン推力を、
「F100ターボファンの計算-2「高空飛行推力」」で、高空、前進速度をもつ飛行状態のエンジン推力を計算しました。
計算結果は実機資料値に近いもので、「悪くはありません。」(ブログ作者個人感想)
しかし、計算-2のF-15Aフライトエンベロープには、個人感想で「これは、ちょっと・・・」の課題が存在します。
投稿履歴、お問い合わせは、「航空 機動/兵装 サイトマップ」へ
「上昇限度が実機より2,000~3,000m高い」
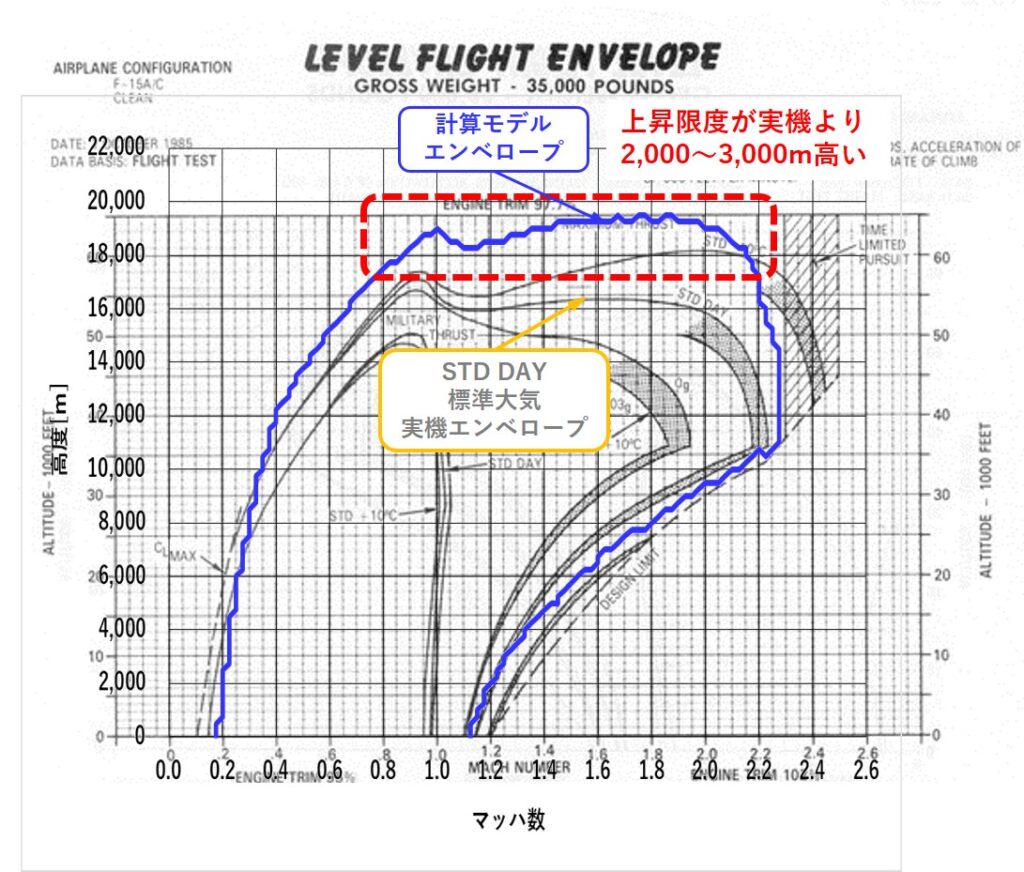
図1.F100-PW-100搭載F-15A計算モデルと実機資料のフライトエンベロープ比較
出典:https://www.c-130.net/forum/viewtopic.php?f=36&t=59015&p=478367
計算モデルの上昇限度を悪くする方法
高度18,000mを飛行不能な領域にする方法として、
空力では、
・最大揚力係数を小さくする
・有害抗力を大きくする
・誘導抗力を大きくする
が、ありますが、揚力1G水平直進飛行のフライトエンベロープなので、最大揚力係数、誘導抗力をいじっても上昇限度は変わりません。有害抗力を大きくすると飛行領域全体へ影響し、フライトエンベロープ下辺が上にシフトして※1全体のバランスを壊します。
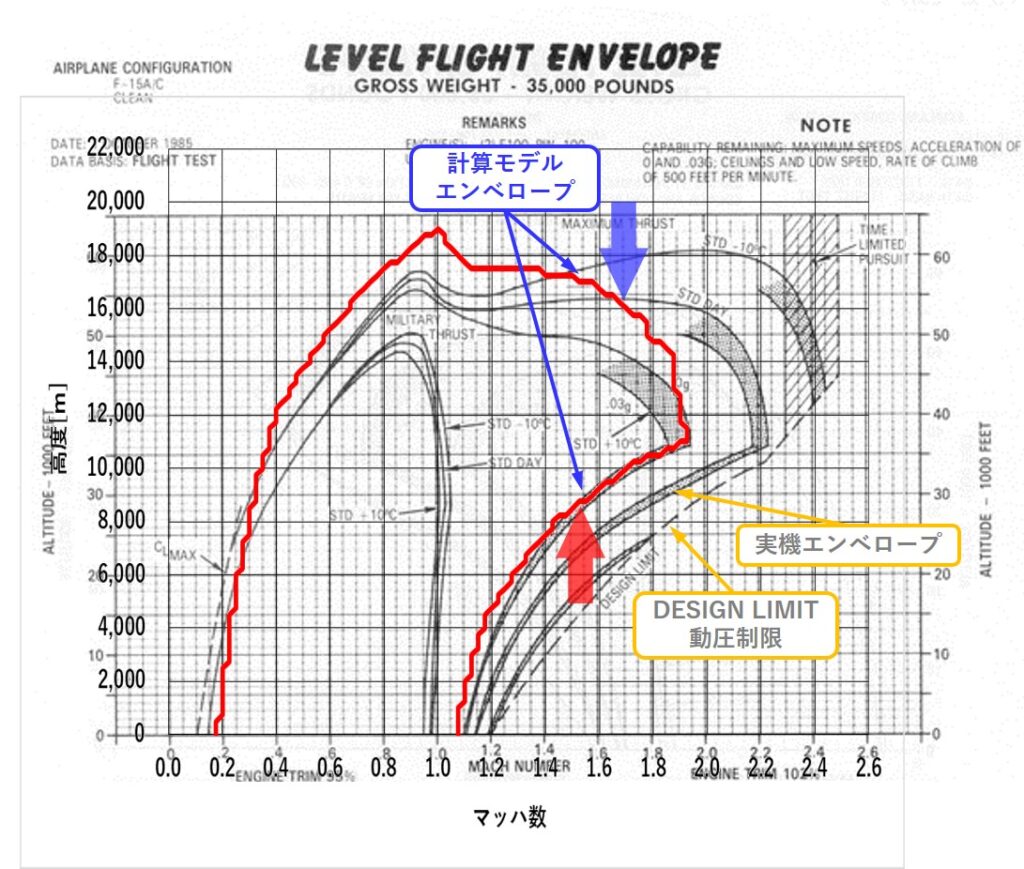
図2.超音速領域の有害抗力を増加させた計算モデルのフライトエンベロープ
※1.超音速領域のフライトエンベロープ下辺は動圧制限によるものではなく、推力限界によるものです。これは、実機エンベロープも同じで、動圧制限ラインの内側にエンベロープがあります。
では、エンジン側の見直しアイテムは、
・ノズル膨張率
・A/B温度
ノズル膨張率は、全飛行領域で等しく「ノズル入口圧力/大気圧力」にしています。この膨張率を高度でいじれば上昇限度を減らせるのでは?※2
なりませんでした。
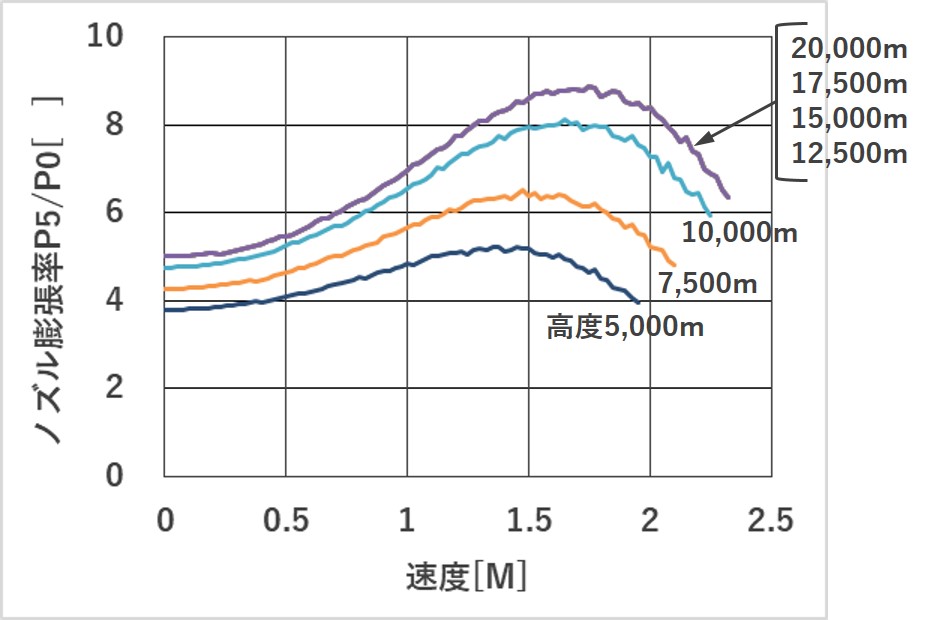
図3.ノズル膨張率の高度による推移
「F100-PW-100ターボファンの計算-2」の「図1.国際標準大気に準じた計算モデルの高度による推移」に示すよう高度11,000m以上は成層圏になり、大気温度は-56.5℃で一定になります。このため、エンジン内の圧力と大気圧との相対変化は一定になり、比率であるノズル膨張率P5/P0も一定になります。高度16,000m以上の膨張率に手を加えれば、高度11,000mまでの領域も影響を受けます。
計算モデルのA/B温度は、高度、速度の全領域で一定としています。しかし、アフターバーナーの冷却(例えばファン流の空気層など)が高度で異なり、高度でA/B温度に差を生じさせるのは?
その後が続きませんでした。
※2.この思考は、工学原理、物理原則を無視して、ただただ計算結果と実機の一致が目的になっています。
レイノルズ数
全高度で一定、あるいは高度16,000m以下も含む領域で一定となるモノではなく、全高度で変化していくモノでなければ、上昇限度の補正はできません。
高度で推移し、「ジェットエンジン」:鈴木弘一:森北出版の索引にある物理量として「レイノルズ数」があります。
「レイノルズ数は層流や乱流のように異なる流れ領域を特徴づけるためにも利用される。
層流については、低いレイノルズ数において発生し、そこでは粘性力が支配的であり、滑らかで安定した流れが特徴である。
乱流については、高いレイノルズ数において発生し、そこでは慣性力が支配的であり、無秩序な渦や不安定な流れが特徴である。」(出典:Wikipedia「レイノルズ数」)

出典:Wikipedia「レイノルズ数」
ρ(密度)は高度で変化します。高度が高いほど大気の密度は減り、レイノルズ数は低くなります。
しかし、前述Wikipediaでは、「層流については、低いレイノルズ数において発生し、そこでは粘性力が支配的であり、滑らかで安定した流れが特徴である。」
・・・? 高度が上がるほどエンジンには良さそう?
とはならず、どうやら高度1,8000mくらいまで上がり密度が地上の10%になると(レイノルズ数の桁が変わると)、圧縮機、タービンに悪い影響が出るようです。
「レイノルズ数変化の効果は、大型エンジンでは比較的小さい。しかし小型エンジンでは特に高々度において、レイノルズ数の低下により圧縮機初段やタービン後段の流れが層流剥離を起こして、性能の大きな劣化を生じる可能性がある。」
出典:「航空宇宙工学便覧」:日本航空宇宙学会 編:丸善出版
:B3 推進機関 B3.2 ターボジェットおよびターボファンエンジン
レイノルズ数の計算モデルへの組み込み
圧縮機入口、タービン入口のレイノルズ数における、海面上、静止状態と高空、飛行状態の比率Re/Rea(添え字a:地上標準状態 添え字無し:高空運転状態)の形で計算モデルへ組み込みます。
レイノルズ数定義式の各要素を、計算モデルでは以下で扱います。
Re=ρvL/μ
v:流体平均速度 →M数一定から音速に比例し、温度^0.5に比例
L:特性長さ →固定
μ:流体の粘性係数 →温度^0.5に比例、圧力非依存
ρ:流体密度 →n/V=P/(R*T)から圧力/温度に比例
これから、
Re ∝ P/T*T^0.5*1/T^0.5=P/T
Re/Rea=(P/Pa)/(T/Ta)
レイノルズ数の圧縮機、タービンへの影響
「レイノルズ数」「圧縮機」「タービン」で検索していくと、
「以上のように、研究者によって多少の違いがあるものの、大部分は、
・損失や効率に対するレイノルズ数の影響は、レイノルズ数の-0.2乗に比例する。
・高レイノルズ数では、レイノルズ数の影響は非常に少なくなる。
という結論にまとめられる。「損失はレイノルズ数の-0.2乗に比例する」ということは、平板上の乱流境界層の厚さがレイノルズ数の-0.2乗に比例して発達することを併せてみれば、物理的にも妥当な考えである。」
出典:「低レイノルズ数域における環状タービン翼列特性」:松沼孝幸
とあります。これから、レイノルズ数の影響は、「-n乗」とします。
計算モデルにおけるレイノルズ数補正の適用
「ジェットエンジン」:鈴木弘一【数値例4.2】を元にする計算モデルの圧縮機、ファン、タービンは、圧力損失ではなく等エントロピー効率ηを使用しています。
性能諸元の効率ηは海面上、静止状態での値とし、高空、飛行状態での効率ηは以下の補正を適用します。
η[%]=(100-(100-ηa)*(Re/Rea)^(-n))
=(100-(100-ηa)*((P/Pa)/(T/Ta))^(-n))
(添え字a:地上標準状態 添え字無し:高空運転状態)
T、Pは、圧縮機、ファン、タービン入口の全温、全圧。
ただし、(P/Pa)/(T/Ta)が1以上(高レイノルズ数)の時は適用しません。
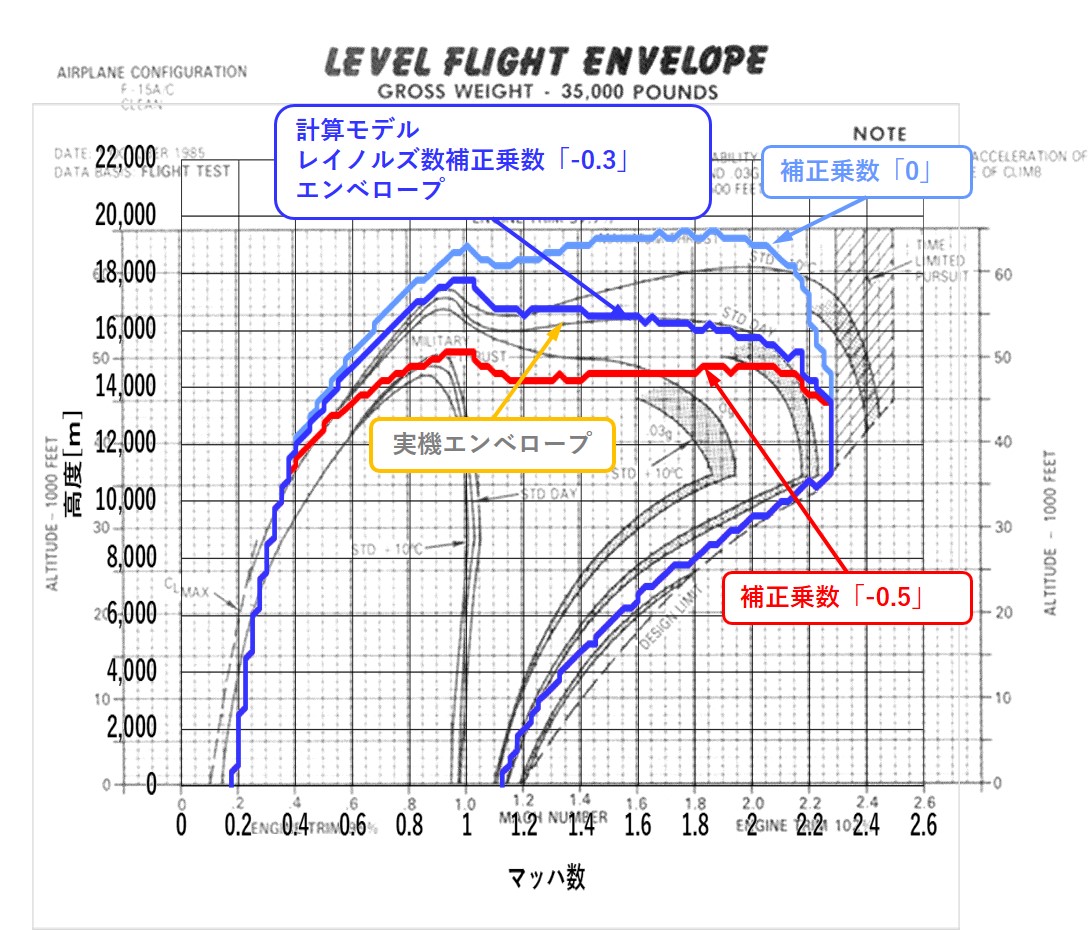
レイノルズ数補正を適用したフライトエンベロープ
レイノルズ数補正を計算モデルへ組み込み、補正乗数「-n」をパラメータとして振ると、
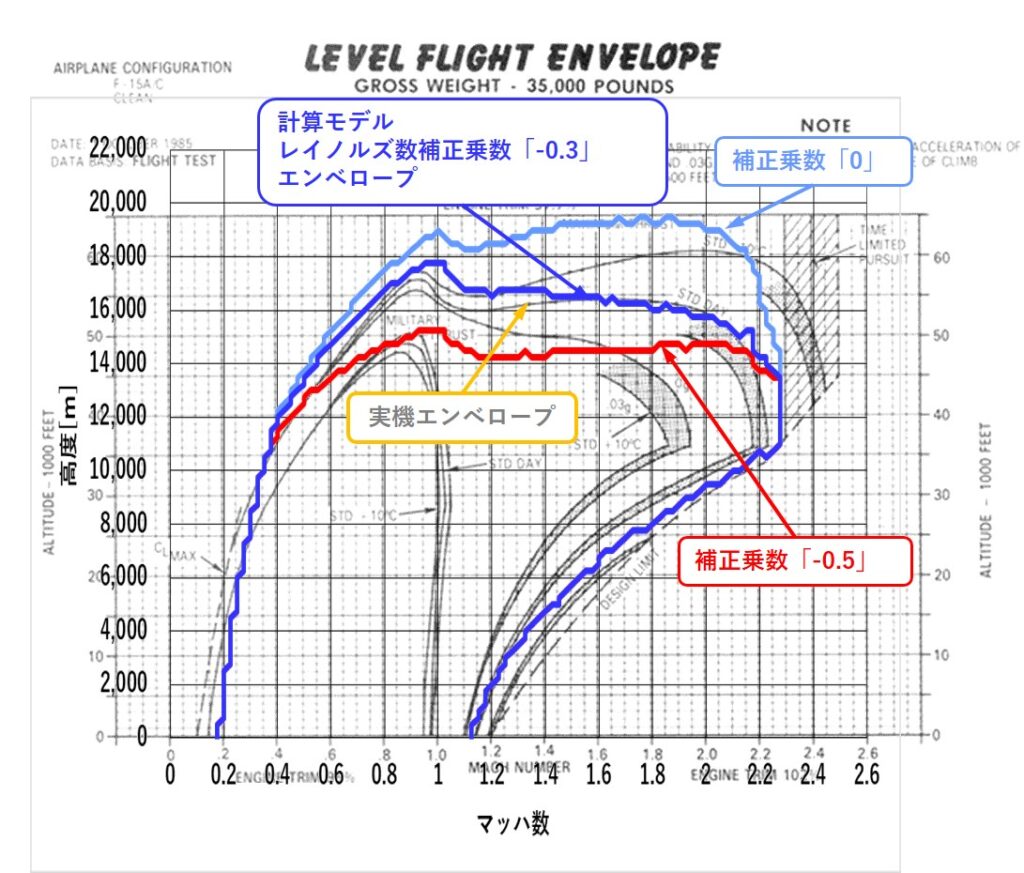
図4.レイノルズ数補正をしたF100-PW-100搭載F-15A計算モデルと
実機資料のフライトエンベロープ比較
所感
低レイノルズ数による圧縮機、ファン、タービンの効率低下の補正を加えることによって、計算モデルエンベロープは実機資料エンベロープに近づきました。
今まで、レイノルズ数と航空機の組み合わせの知見は「火星探査飛行機」くらいだった所に、
「高々度大気の低レイノルズ数に起因するエンジン性能低下によりF-15Aの上昇限度が2,000~3,000m低下する。」となっても、「信じるか、信じないかは、・・・」の世界です。
今後、SR-71、MiG-25のフライトエンベロープの作成で、レイノルズ数補正が生き残れるのか、(趣味の計算モデルにとっては)有効性があるのか、または何らかの一次資料が見つかるのか、検証を進めます。