航空機の機動、戦闘機のドッグファイトをシミュレートする
ドッグファイトシートのスケールの説明
前回「ドッグファイトシートによる機動のシミュレート」で、ドッグファイトシート(水平飛行)を紹介しました。
その中のスケールについて説明します。
投稿履歴、お問い合わせは、「航空 機動/兵装 サイトマップ」へ
「ドッグファイトシート」
ヘックス(六角形)シートを使用して、定量的に飛行をプロットするツール
1ヘックス:250m 1ターン:5秒 速度ポイント:50m/s=100kt(ノット)
1Gの1ターン後の速度変化量:1速度ポイント
1G旋回でのターン終了時のヘックス移動量:1ヘックス
詳細およびヘックスシート.pdfのダウンロードは、本ブログ「ドッグファイトシートによる機動のシミュレート」参照
ヘックス間距離250mと1ターン5秒および加速度1Gの関係
ドッグファイトシートにおける飛行は、航空機に働く4つの「力」(揚力、抗力、エンジン推力および重力)を機体重量で割った4つの「加速度」で管理します。
(重力は、機体速度方向の成分と、機体速度直交方向の成分に分割されます。)
「加速度」の単位は、「G」(重力加速度:9.806m/s^2)を使用します。
機体速度と直交する方向に働く揚力、重力成分と機体速度方向に働く抗力、推力、重力成分の加速度すべてを「G」で扱います。
機体速度方向に働く1Gの加速度は、1ターン5秒間で速度を、
9.806m/s^2x5s =49.03m/s
加減速させます。
49.03m/s ≒50m/s※1として速度ポイントは50m/秒を採用、
速度50m/sは1ターン5秒間に250m進むので、ヘックス間距離は250mになります。
50m/sは、180km/時であり、100ノット(185.2km/時)と近似するので、
速度ポイントは、(公称)100ノット(100kt)としています。
※1.ドッグファイトシートの1Gは、10m/s^2の世界線です。
旋回ルール
・旋回する場合、ターン終了時の未来位置ヘックスを起点として、
旋回のG数分、ヘックス移動させます。
・左右への移動は、開始ヘックスを中心とし、移動ポイントを半径とする円周上
(ヘックスシートでは六角形となるヘックス列上)になります。
・旋回G数分のヘックス移動は、どの速度ポイントでも同じく適用されます。
速度ベクトルで考えます。
1ターン中に1Gの加速度が働くと1速度ポイントの速度ベクトル(1ヘックス分)になります。
ターン終了時の速度ベクトルは、ターン開始時の速度ベクトルと
加速度により生じた速度ベクトルとを合成したものになります。
旋回Gは、機体速度方向と直交する揚力(と重力成分)によるものなので、ターン開始時の速度ベクトルと直交する方向の速度ベクトルの合成になり、上記の旋回ルールになります。
円運動の公式(F=mv^2/r=mrω^2)で考えます。
円運動の公式を質量で割り、加速度で扱うと、
F/m=v^2/r=rω^2
F/m:向心加速度 v:速度 r:半径 ω:角速度(単位はラジアン/秒)
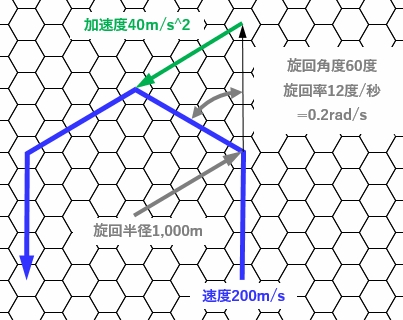
ドッグファイトシートでは、速度ポイントn、旋回nGの場合、
1ターン(5秒)に、60度旋回し、旋回半径nx250mになります。
これは、速度nx50m/s、加速度nG=nx10m/s^2、旋回率12度/秒=0.2rad/s※2、
旋回半径nx250mの円運動であり、円運動の公式が成り立ちます。
※2.ドッグファイトシートのπ(円周率)は、3の世界線です。
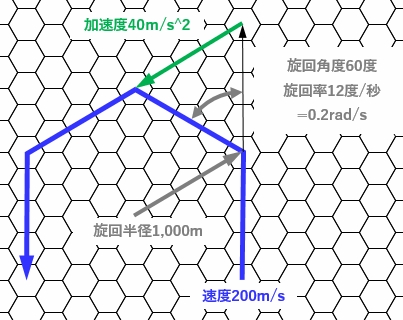
図1.ドッグファイトシートにおける、速度ポイントn、旋回nGの旋回率、旋回半径
(図は、n=4の場合)
最後に
今回は、多数の数式で申し訳ありません。
カテゴリー「ドッグファイトシート」の次回は、図を多用して、ドッグファイトシステムの旋回と実機の旋回との比較を行います。
”すごろく”をして、本当にシミュレーションになっているの?