エネルギー機動ダイグラムを、上昇率[feet/s]以外の単位でプロットする
エネルギー機動ダイアグラムでプロットされるPs(エネルギー比率)の単位は[feet/s]([ft/s])ですが、エクセル(Microsoft Excel)の計算モデルでは、他の単位でのダイアグラム作成が可能なので、Psのバリエーションを作成します。
投稿履歴、お問い合わせは、「航空 機動/兵装 サイトマップ」へ
エネルギー機動ダイアグラムの事例
一例としてF-15のエネルギー機動ダイアグラムを示します。
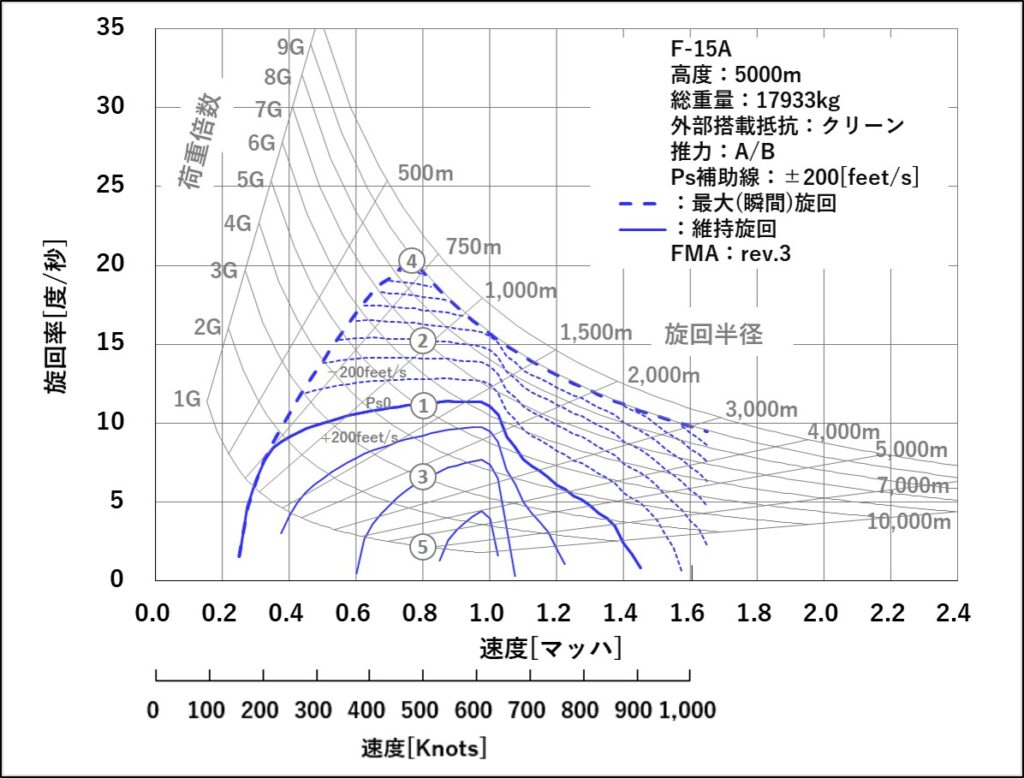
エネルギー機動ダイアグラムは、特定の高度における航空機の旋回性能とエネルギー状態を示すものです。
旋回性能
・荷重倍数[G]:左上から右下への曲線
・旋回率[度/秒]:ダイアグラム縦軸
・旋回半径[m]:左下から右上への直線
・速度[マッハ]:ダイアグラム横軸
・最大旋回:最大揚力での旋回、維持旋回より上の場合、減速、降下が発生するので、
そのGでの旋回は瞬間になる。
・維持旋回:最大推力で、減速、降下が無く、増速、上昇が出来なく、継続できる旋回
・ダイアグラム左端:最大揚力による制限、それ以上のGを掛けようとすると失速する
・ダイアグラム右端:機体強度からのG制限
エネルギー状態
・Ps0:維持旋回、機体の発生し得る最大推力を過不足無く使う旋回
・Ps0より上:エネルギー不足、その旋回Gを続けるには、減速、降下が必要
・Ps0より下:エネルギー余剰、旋回しつつ、増速、上昇が可能
・ポイント①のM0.8、5G旋回は、Ps(エネルギー比率)が0付近の旋回で、
旋回率が毎秒11度(180度旋回するのに約16秒)、半径1,341mの旋回を継続して維持できます。
・7Gまで旋回を強めると(ポイント②)、推力<抗力になりPs値はマイナスになります。
損失していくエネルギーの量は、位置エネルギーで表すと毎秒619feetに相当します。
・次に3G旋回に緩めると(ポイント③)Psはプラスになり、
3G旋回をしながら毎秒389feetの上昇ができ、位置エネルギーを獲得できます。
・最大旋回率となる旋回はM0.78での9G旋回(ポイント④)です。
旋回率は20度/秒。旋回半径も704mに縮小します。
ただし、Psは-1,797feet/sまで低下し、エネルギーは著しく損失していきます。
高度の低下(位置エネルギーの損失)は、毎秒1,787feet、mに直すと毎秒539mの落下となります。
??速度は256m/s、539m/sの落下ができる?? できません。
なので、ヴァーティカル・スパイラル・ダイブ(垂直螺旋降下)で最大限、位置エネルギーで支払い
をしても、まだ足りなく減速(速度エネルギーによる支払い)をしていきます。※1
・逆に1G旋回(ポイント⑤)では、毎秒544feet(166m、毎分約10,000m!)の上昇が可能です。
パイロットには①から⑤までの選択の幅があり、Gと闘いながら旋回、上昇、下降、増速、減速を時々刻々と判断していく。これは凄いことですね。
※1.このすさまじいエネルギー損失は、9G揚力にともない発生する誘導抗力の増加が原因です。
が、「F-15のエネルギー機動ダイアグラム修正」にあるよう、誘導抗力の扱いは調査、確認、検証中であり、現時点での計算モデル(FMA rev.3)による結果の位置づけです。
(ちょっと大き過ぎる感があり・・・、「高G旋回による減速」の実機資料が欲しいところです。)
上昇率[m/s]
日本人で高度の単位にフィートに馴染みがある人は、航空機の運航従事者か、フライトシムのヘビーユーザなので、高度の単位をmにします。
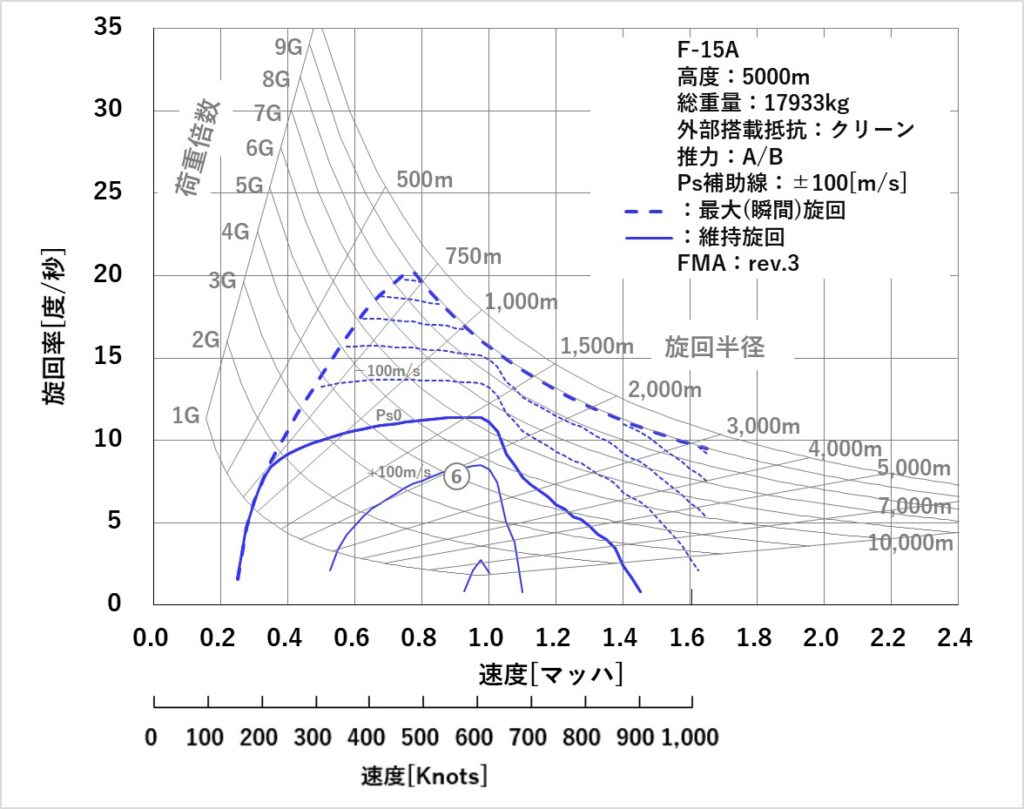
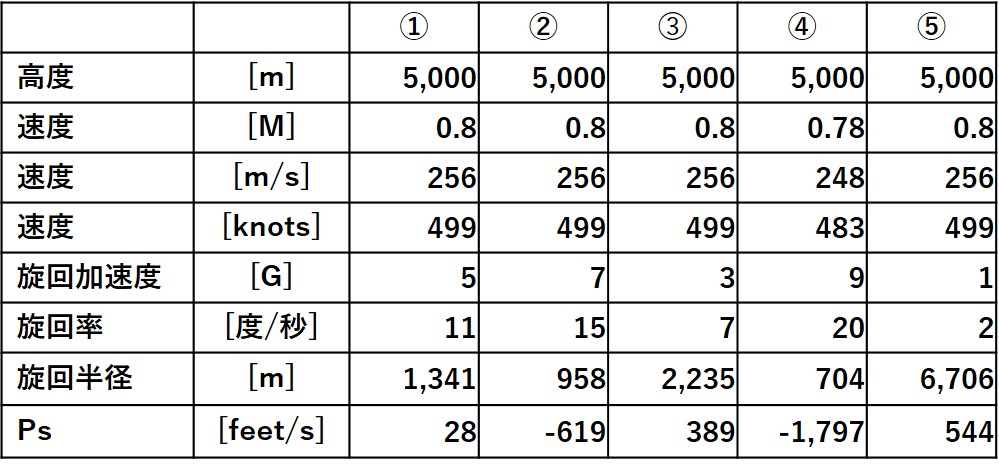
[feet/s]と補助線の間隔が異なるだけですが、「旋回を1G増加すると、旋回率は2度/秒増加するがPSは-100mになる。対抗機と1,000mの高度差があるので10秒間降下して20度の増加を得ることができる。」と、直感的に分かります。
Psプラス値の旋回中の上昇ですが、以下の資料と比較します。マッハ0.9、4G旋回のポイント⑥は、旋回率7.8度/秒なので180度旋回に23秒掛かり、Ps+111m/sから2,553m上昇するので、概ね一致します。
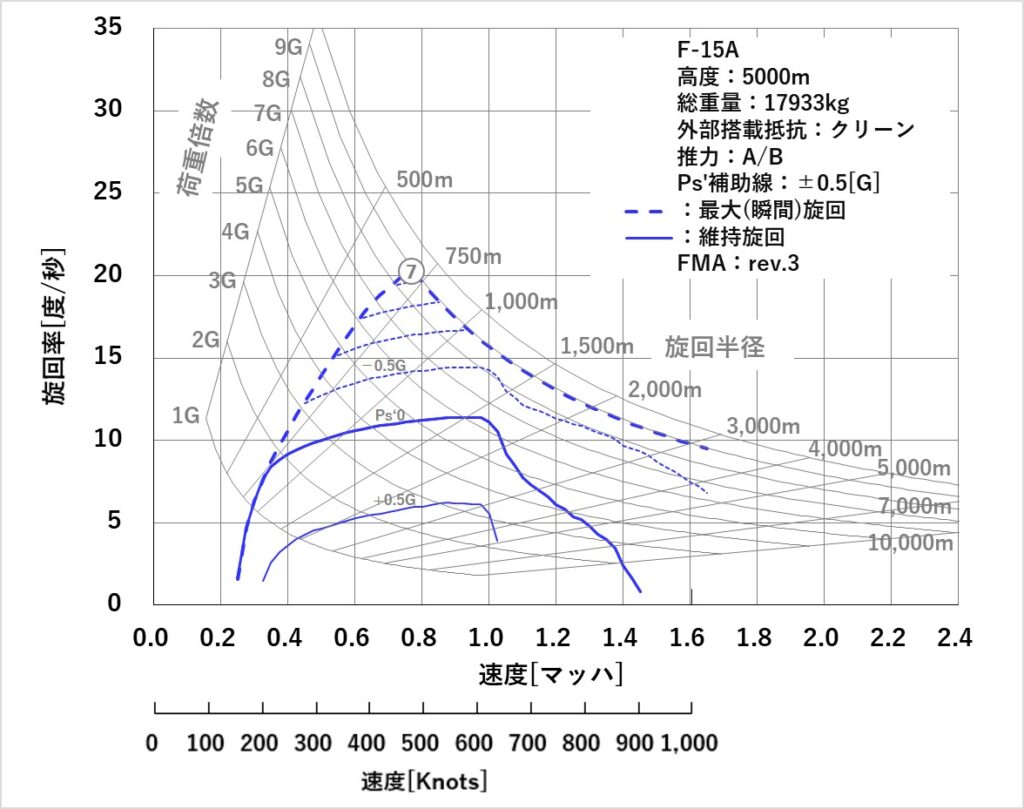
加速度[G]
Psの式から(T-D)/Wを取り出します。(T-D)/Wは、加速度であり「余剰推力重量比」と言えるものです。単位は[G]を使用します。※2
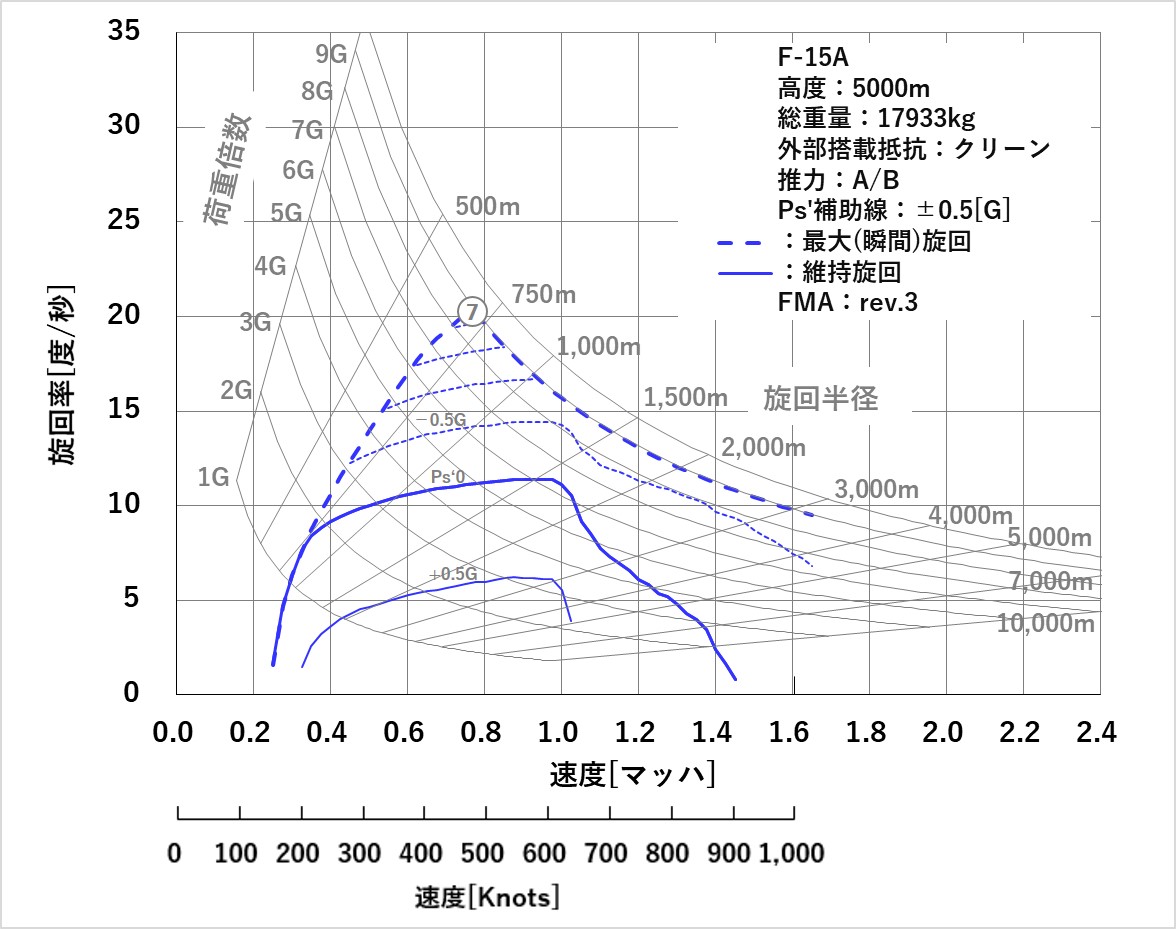
ダイアグラムのラインは上昇率と微妙に異なるものですが、最大旋回率(ポイント⑦、図1の④)のPs’[G]は-2.2Gになり、前述の垂直降下しても減速する状態とリンクします。
※2.上昇率[m/s]は、単位を換えただけで物理量[高度/時間]は変わりませんが、加速度は物理量が変わるので「Ps’」と表記します。
なお、Ps’(加速度)は、当然ながら、まったくの非公認、一個人の趣味の世界の産物です。
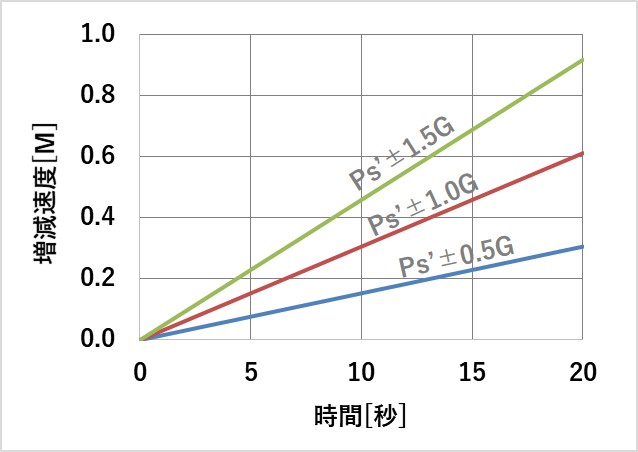
加速度からは、1秒間にどの程度、速度が増速、減速されるのかが分かります。
また、(T-D)/Wは、最大上昇角θのsinθになるので、余剰推力重量比と速度の増減および上昇角度の関係を示すグラフも追加します。

所感
加速度[G]の方が余剰推力、誘導抗力による減速の度合いが分かり、スロットル操作を含む操縦に結び付きます。上昇率は旋回と高度との変換比率(交換レート)が分かり、何秒後の見通しを立てることができるので、機動のマネージメントに結び付くことになると考えます。